Single linked list with circle
This is a classical interview question, but it is very useful in practice as well. So let’s discuss it here in detail. The problem is like this:
Given a single linked list, how to determine whether it has a circle or not?
The solution is intuitive: point two pointers, fast and slow, to
the head of the list, then use them simultaneously to traverse the
list. fast and slow advance m and n steps each time
respectively, . If slow catches up with fast before
fast reaches the end of the list, we can claim that there is a
circle in the list.
It is obvious that slow will never catch up with fast if the list
has no circle, i.e. . Now
let’s prove that slow will finally catch up with fast if the list
indeed has a circle, i.e. .
Suppose the list is composed of a linear part and a circle, the length
of which are l and c respectively. Assume slow catches up with
fast in s steps, then we have . Put this in another way:
Solve the equation we get
There is nothing to stop us to pick up p and q such that . So s has at least one solution, ,
which satisfies all the constrains below:
Therefore slow will catch up with fast in steps,
though this is not necessarily the first time they meet again.
So we just proved . Now comes the follow up question:
How to find the beginning of the circle?
Let A be the head of the list, B be the beginning point of the
circle, and C be the catch up point of slow and fast, then the
list looks like this:
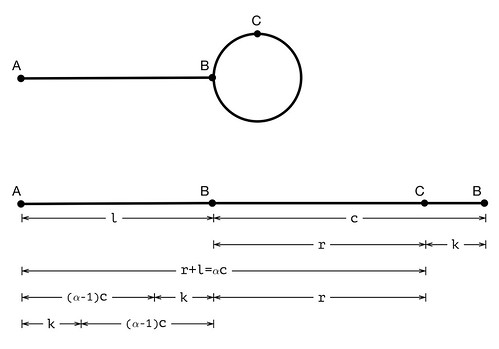
If we choose m=2 and n=1, solve the equation above we can get
l+r=(p-2q)c. Let α=p-2q, then l+r=αc, l=αc-r=(α-1)c+k. Now we
put a pointer p0 on A, a pointer p1 on C, then advance them 1
step every time. After k steps, p0 is (α-1)c steps away from
B, but p1 reaches B already. Therefore, after (α-1)c more
steps, p0 and p1 meet with each other on B.